Optimizing Circle Placement in a Defined Area: A Pyomo-Based Approach
In various scientific and engineering applications, there is a need to optimally arrange objects within a given space. One fascinating instance is the problem of placing multiple circles within a rectangular area to maximize the covered area without overlapping. This task is highly relevant in experiment design. In this post, I explore a Python-based approach using the Pyomo optimization library to solve this problem.
Background
The circle placement problem can be categorized as a type of packing problem, which is a well-known challenge in operations research and combinatorial optimization. The primary objective is to arrange a set of circles within a bounded area such that the total covered area is maximized and no circles overlap.
Why This Is Useful
Optimal placement of objects is crucial in many fields:
- Experiment Design: Efficient use of space can lead to better experiment setups and resource utilization.
- Manufacturing: In industries, optimizing the layout of components can minimize waste and reduce costs.
- Urban Planning: Placing structures optimally in a given area ensures better space utilization and accessibility.
The Python Code
The Python script that uses Pyomo, a popular optimization library, to solve the circle placement problem is available on my Github. The code creates a model, defines constraints to prevent overlapping, and ensures circles stay within the boundaries. The solution is obtained by testing multiple initializations to find the best arrangement.
Explanation of the Code
Defining the Area and Parameters:
- The area dimensions are defined using
AREA_WIDTHandAREA_HEIGHT. - The number of circles (
NUM_CIRCLES) and the number of initializations to test (NUM_INITIALIZATIONS) are set.
Creating the Model:
- The
create_model()function defines the Pyomo model. - Variables
x,y, andrrepresent the x-coordinate, y-coordinate, and radius of each circle, respectively. - The objective is to maximize the total area covered by the circles.
- Constraints are added to prevent overlap and ensure that circles stay within the defined area.
Solving the Model:
- The
solve_model()function uses the IPOPT solver to solve the model. - Multiple initializations are tested to find the best solution.
Calculating Coverage and Visualization:
- The best solution is selected based on the maximum covered area.
- The coverage percentage is calculated and displayed.
- The final positions of the circles are plotted using Matplotlib.
Results
An example output from running the code might look like this:
Coverage rate: 85.91%
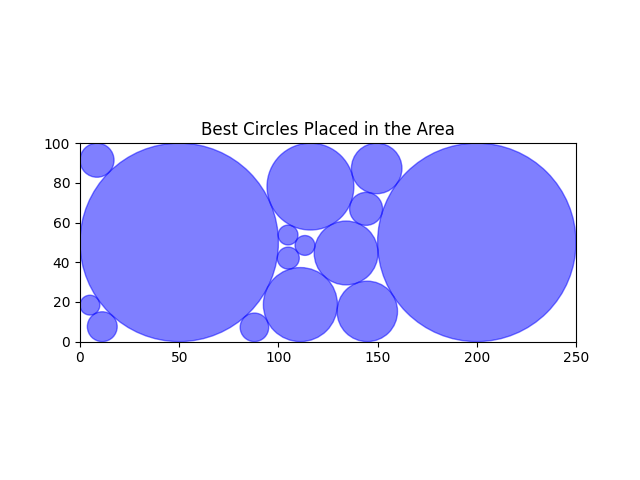 I'm still far from this solution! It's important to note that due to the complexity of the circle packing problem, the solution found may not always be fully optimized. Different initializations and solvers can yield varying results. On this example there is still a lot of space on the right hand corners.
I'm still far from this solution! It's important to note that due to the complexity of the circle packing problem, the solution found may not always be fully optimized. Different initializations and solvers can yield varying results. On this example there is still a lot of space on the right hand corners.
Conclusion
This Pyomo-based approach provides a powerful method to tackle the circle packing problem efficiently. By leveraging optimization techniques, it ensures that circles are placed optimally within a defined area, maximizing the area covered while adhering to specified constraints. Such techniques are really pertinent in experiment design, logistics planning, and other domains where efficient space utilization is crucial.
For further exploration:
- Pyomo Documentation: Pyomo
- IPOPT Solver Documentation: IPOPT
- inspiration: yetanothermathprogrammingconsultant