Combining Models for Better Predictions: Stacking in Machine Learning
What is Stacking?
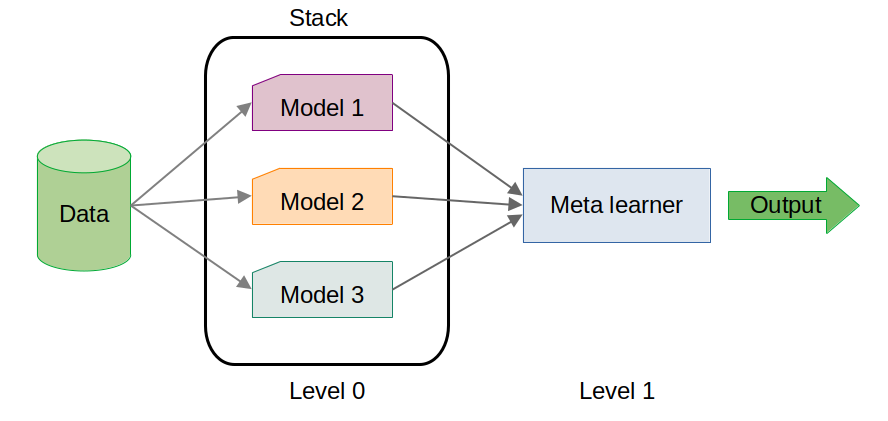
Stacking is an ensemble learning technique that combines the predictions of multiple base models (level 0 models) to generate a final prediction using a meta-model (level 1 model). Unlike simple voting or averaging methods, stacking uses a meta-model to learn how to best combine the predictions of base models, thereby capturing complex patterns and relationships in the data.
How Stacking Works:
Base Models (Level 0 Models): These are the individual models that are trained on the same dataset. They could be of different types, such as a decision tree, a k-nearest neighbors model, or a support vector machine.
Meta-Model (Level 1 Model): The predictions of the base models are used as features to train a meta-model. This model learns the optimal way to combine the base models' predictions to improve accuracy.
Final Prediction: The meta-model produces the final prediction by integrating the predictions of the base models.
Why using Stacking?
Improved Performance: By combining multiple models, stacking can often outperform any single model. It leverages the strengths of each base model while mitigating their weaknesses.
Flexibility: Stacking allows you to combine different types of models, making it versatile for various datasets and problems.
Reduced Overfitting: The meta-model can learn to generalize better by combining the predictions of overfitted base models, leading to a more robust final model.
The main drawback of Stacking is the training time. It’s computationally expensive and time-consuming, especially for large datasets.
Practical Example: Stacking in Action - Predicting Poisonous Mushrooms on Kaggle
For this practical example, we'll walk through how I used stacking to participate in the Kaggle competition Playground Series - Season 4, Episode 8: Binary Prediction of Poisonous Mushrooms. The goal of the competition is to predict whether a mushroom is edible or poisonous based on its physical characteristics.
I'll skip the loading and pre-processing parts that you can find in my jupyter notebook.
Once the data are correctly formatted, I trained three different models as the base learners:
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
# Initialize classifiers
rf = RandomForestClassifier(n_estimators=100, random_state=42, n_jobs = -1)
gb = GradientBoostingClassifier(n_estimators=100, random_state=42)
knn = KNeighborsClassifier(n_neighbors=5)
# Train classifiers
rf.fit(X_TRAIN, Y_TRAIN)
gb.fit(X_TRAIN, Y_TRAIN)
knn.fit(X_TRAIN, Y_TRAIN)
# Predict on the validation set
y_pred_rf = rf.predict(X_VAL)
y_pred_gb = gb.predict(X_VAL)
y_pred_knn = knn.predict(X_VAL)
To enhance the prediction accuracy, I combined these base models using a stacking approach:
from sklearn.ensemble import StackingClassifier
# Define base learners
base_learners = [
('rf', rf),
('gb', gb),
('knn', knn)
]
# Define meta-learner
meta_learner = LogisticRegression()
# Initialize Stacking Classifier
stacking_clf = StackingClassifier(estimators=base_learners, final_estimator=meta_learner)
# Train Stacking Classifier
stacking_clf.fit(X_TRAIN, y_train)
# Predict on validation set
y_pred_stacking = stacking_clf.predict(X_VAL)
Finally, I evaluated the performance of each base model and the stacked model on the validation set to see the benefits of stacking:
from sklearn.metrics import matthews_corrcoef
# Calculate mcc for each model
mcc = {
'Random Forest': matthews_corrcoef(Y_VAL, y_pred_rf),
'Gradient Boosting': matthews_corrcoef(Y_VAL, y_pred_gb),
'KNN': matthews_corrcoef(Y_VAL, y_pred_knn),
'Stacking': matthews_corrcoef(Y_VAL, y_pred_stacking)
}
# Sort MCC values for better visualization
sorted_mcc = dict(sorted(mcc.items(), key=lambda item: item[1]))
# Plot the MCCs
plt.figure(figsize=(10, 6))
bars = plt.barh(list(sorted_mcc.keys()), list(sorted_mcc.values()), color=['#3498db', '#2ecc71', '#e74c3c', '#9b59b6'])
# Add MCC values to the bars
for bar in bars:
plt.text(bar.get_width() + 0.01, bar.get_y() + bar.get_height()/2,
f'{bar.get_width():.3f}', va='center', fontsize=12)
plt.xlabel('Matthews Correlation Coefficient (MCC)', fontsize=14)
plt.title('Comparison of Base Models and Stacking Model', fontsize=16)
plt.xlim([0., 1.06])
plt.grid(axis='x', linestyle='--', alpha=0.7)
plt.show()
In this Kaggle competition the performance is evaluated using Matthews Correlation Coefficient (MCC). It is a metric for binary classification that takes into account true and false positives and negatives, providing a balanced measure even when the classes are imbalanced.
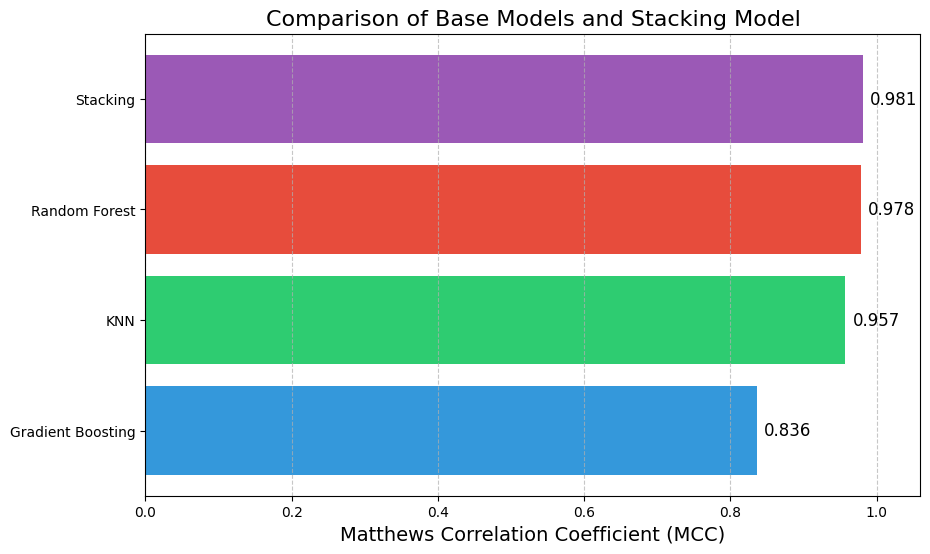Here, the stacking model slightly outperformed the individual base models. While the improvement may seem marginal, in high-stakes scenarios, even small gains in performance can be critical.
Credit: Yakfish Taco
Credit: Janusz Szwabiński
